在三维空间里,用的最多的视角就是第一人称和第三人称,由于在3d模型中,基本都是基于人眼进行模拟的,所以第一人称相对更容易实现,因为人眼就是camera,而我们本身(或者说是人眼)的位置就是camera.position,而人眼的直视方向就可以是camera的direction。
由于three.js里面的概念比较清晰,也比较接近实际,所以可以很容易实现。首先,我们可以假定我们所在的3d空间为一个球体,球体的边缘即“无穷远处”为天空(当然,现实中有地平线,暂且不讨论),因此可以利用数学当中的球坐标系进行计算,只需要三个变量r(即球体半径),α(即竖直方向角,在three.js中及视觉方向向量与xz平面的夹角,范围为-π/2 ~ π/2),β(即水平方向角,可以看做xz平面内的极坐标角,我设定的起始方向为z轴的负方向,沿顺时针旋转,范围为0 ~ 2π)。需要说明的是这个r并非空间球体的那个半径,而是基于camera的position所自定义的球体(其实这个r大小无关紧要,设为单位大小即可)。
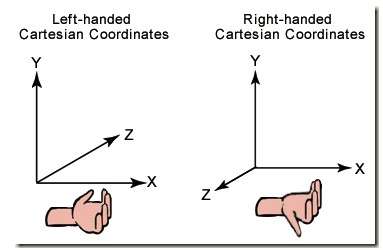
首先需要了解canvas的坐标轴与three.js的坐标轴的设定:
右边的即为three.js的坐标系设定。
接下来就是该怎么计算这3个变量(其实是两个,r可以进行预设)的值的问题了,这涉及到的是canvas画布的mousemove事件,由于mousemove事件会传递其坐标给event,由于three.js的坐标系决定了我们看到屏幕上的实际是xy平面,因此可以将(width/2 , height /2)设为我们的参考原点(即初始参照,α为0 ,β为0),然后根据event.x,event.y(我这里指的是全屏状态或100%宽度时)相对于(width/2 , height /2)距离进行计算。具体计算公式如下:
α = (height / 2 – y)/ (height / 2) * (π/2)
β = (x – width / 2)/(width / 2) * π
然后就可以算出视角的方向向量:
Vx = r *cosα* sinβ
Vy = r *sinα
Vz = r *cosα* cosβ
目前我还不清楚是否有直接设置camera的方向的函数,所以我使用了camera的lookAt方法设置方向。看个例子吧:
var ex = 10 * Math.cos(alpha) * Math.sin(beta); var ey = 10 * Math.sin(alpha); var ez = - 10 * Math.cos(alpha) * Math.cos(beta); var e = new THREE.Vector3(camera.position.x + ex , camera.position.y + ey , camera.position.z + ez); camera.lookAt(e); renderer.render(scene , camera);
如果进行移动的话(即改变x,y,z值)时,需要将camera的position及时保持与“我”的位置一致即可。




发表回复
要发表评论,您必须先登录。