原理

首先根据迷宫的行列大小构造迷宫的基本轮廓，然后其中的每一方格代表一个结点（如图中圆点），每个结点的初始邻接点按4-连通的方式构造；

然后给每个边（即相邻的两点）给定随机生成的权重，根据这些点和带权重的边找出该图的最小生成树（理论上只需要找出任何一个生成树即可！），常用的查找MST的算法是Prim和Kruskal；图中带颜色的边即为最小生成树的边。

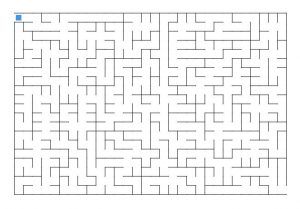
根据得到的最小生成树所包含的边，在这里的边可以看做某两点是处于连通的状态！因此，只需将连通的两点之间的“墙”拆掉即可得到一个随机迷宫，这里的“墙”指的就是之前画的基本框架中的格子线……

没错，这就是拆墙法构造迷宫。

后话：如何判定迷宫中走的每一步是否“穿墙”呢？很简单，利用得到的最小生成树构成一个新图，如果从该点走出的下一步不属于该点的邻接点即为“穿墙”！

 

---

在用js实现Prim和Kruskal算法时遇到了运行时间的问题，貌似用很直白的Prim的算法查找几百个结点的MST确实很费时；于是想到用Kruskal算法，但是在实现Kruskal算法的判定加入一条边是否使图形成环的时候有点被卡住了，想到的也是很费劲的暴力循环，然而无意间在网上看到的一个Kruskal算法实现，简直就是被震撼到了！

var E = [];
<pre>var vest = [];// 连通集标识符号，代表各点所属的连通集
var otherE = _this.edgeList.slice(0);
var edgeNum = _this.nodeList.length - 1;

for(var n = 0; n < edgeNum + 1; n++){
    vest.push(n);// 初始化连通集符号，各点在最初时各自为不同的连通集
}

while (E.length < edgeNum){
    var minIdx = 0;
    var minWeight = 10000;

    for(var k in otherE){// 查找剩余边集中权重最小的边
        if(otherE[k].w < minWeight){
            minIdx = k;
            minWeight = otherE[k].w;
        }
    }

    var minEdge = otherE[minIdx];
    otherE.splice(minIdx, 1);// 删除当前最小边
    // 算法参照 https://www.cnblogs.com/wxdjss/p/5503023.html
    var sn1 = vest[minEdge.a];
    var sn2 = vest[minEdge.b];
    if(sn1 != sn2){// 判断最小边的两点所属连通集是否相等，不相等即可加入，即判断该边加入是否构成环！！！
        E.push(minEdge);
        for(var i = 0; i < edgeNum + 1; i++){// 该边加入时，则代表该边的两点所属的连通集连通了！！！
            if(vest[i] == sn2)
                vest[i] = sn1;
        }
    }
}

这个算法的精妙就在于用连通标识符来判定一条的两点是否属于同一连通集，属于同一连通集加入该边即会构成一条环！这让我认识到同一算法的实现是存在很大的差异，效果也是相差很大！想要写出这样短小精悍，一针见血的算法实现看来还得多下点功夫啊……

Codepen地址：https://codepen.io/xxf1996/full/GQojzx/