最近正好在研究unity3d的AI人工智能的一些算法,主要是借阅了学校图书馆的一本叫做《unity3d人工智能编程精粹》的书,里面涉及方面不是很多,但每个例子都讲得非常的细致,刚好可以作为入门书籍看看。里面有一章就讲到了导航寻路,提到了A*算法。虽说u3d里有个A*的插件,但我还是想自己实现一遍。
借着前几天在canvas实现的几个光栅画线的模板,这次也想用网格在canvas上做个简单的A*的动态寻路的例子。其实思路是比较简单的:
1. 将每个格子(方块)看做一个节点,然后计算并记录该点到目标节点(即终点)的估计距离(我采用简单的曼哈顿距离)h,及离出发节点的代价值(这里我采用对角线方向为1.414,其余为1)g,最后总代价值f = g + h,并记录父节点(即前一节点);
2. 首先从出发点开始(出发点g=0,无父节点),将其加入open表(open list),开始迭代。
3. 检查open表是否为空,不为空则进行迭代;取出open表中总代价f最小的节点,若为目标节点则停止迭代,否则进行相邻节点(可以是4个节点,也可以是8个节点,有点类似于4联通和8联通)的检查。
4. 检查节点:如果既不在open表也不在closed表中,则加入open表中;如果在open表中,则检查新的节点f是否小于旧节点的f值,若小于则更新旧节点为新节点;如果在closed表中,也要检查新节点的f值,若小于旧节点的f值,则把旧节点从closed表中移除,并把新节点加入到open表中。
5. 一次迭代结束后,将此前最小节点加入到closed表中,开始下一次迭代(重复3,4)直到找到目标点或者是open表为空(即无法达到目标点)。
注:在第3步进行检查的时候还要进行必要的碰撞检测,即检查是否为障碍物,不能将障碍点加入到表中,也不能直接穿过障碍物。
优点:这个算法的优点就是一般可以找到最优路线,而且可以进行动态改变。
缺点:缺点也是很明显,这个算法的迭代和循环遍历的次数比较多,只要地图上的节点数一多,所需的时间也会大量增加。并且在无法找到目标点时会迭代地图上所有节点,很浪费时间。
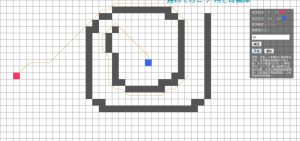
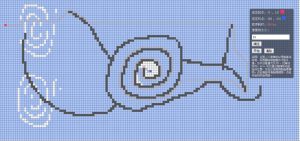
从上图可以看出,当像素块大小为30时进行的一个环形障碍物测试所需时间为3855ms,而在像素块大小为20时在相似位置做相似的测试所需的时间为8211ms。很明显,随着节点的增多,所需的时间也大大地增加了。
说明:由于是用js语言实现的,而这个算法的效率与数据结构有很大的关系,在js中像队列,栈,哈希表都没有支持,而且连动态的二维数组都不支持!!!我在这里仅使用一维数组储存数据,仅仅是最原始的A*算法实现,所以效率大打折扣,估计用java或者c++这些语言实现会好很多。我在网上看了一位大神写的A*的Demo(PathFinding.js),那可是ms级的啊。而且很多地方还可以进行优化,比如需要进行遍历的地方尽量换成不要遍历的方法,open表和close表的结构也可以优化。总之,可以改进的地方有很多,这方面的优化网上也有许多,日后可以深究一下。
更新(2016-10-3)
这里要更正一下,之前在js上运行效率之所以会这么低不是由于js数据结构的原因,而是我自己在循环体中使用了大量的自定义函数 ,而那个自定义函数比较耗时(大概一次循环会耗时10ms左右)。经测试本身的for循环大概不到1ms,所以程序正常耗时应该也就是几十ms到几百ms之间。
,而那个自定义函数比较耗时(大概一次循环会耗时10ms左右)。经测试本身的for循环大概不到1ms,所以程序正常耗时应该也就是几十ms到几百ms之间。
还有,昨天刚好看了一篇关于A*算法的优化的文章(地址没保存 ,所以忘了),里面提到了close表存在的必要性说道closed表完全不必要(或者说是不需要进行遍历判断再更新),于是乎我就把close表去掉,将探索完后的节点进行标记;然后以节点的x,y作为数组的索引,将所有的数组(标记,障碍物,open表)转为一维数组,因此只剩下一处地方有遍历——取得当前open表代价最小节点。然后效率就刷刷的上来了,一以下是一些环形障碍测试:
,所以忘了),里面提到了close表存在的必要性说道closed表完全不必要(或者说是不需要进行遍历判断再更新),于是乎我就把close表去掉,将探索完后的节点进行标记;然后以节点的x,y作为数组的索引,将所有的数组(标记,障碍物,open表)转为一维数组,因此只剩下一处地方有遍历——取得当前open表代价最小节点。然后效率就刷刷的上来了,一以下是一些环形障碍测试:
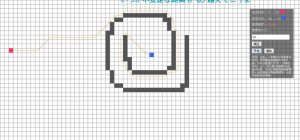
当像素块大小为30时,耗时为92ms:
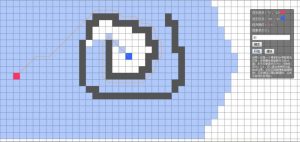
当像素块大小为20时,耗时为366ms:
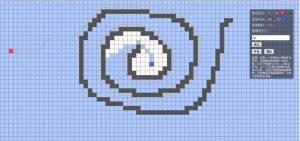
我还试了一下丧心病狂的像素块大小为10时,耗时为3901ms:
当然,这仅仅是一点小小的优化,真正的优化还是对最小代价节点的取舍以及对数据结构的优化方面。
更新(2016-10-8)
由于在网上看到一个比A*算法效率高很多的算法——JPS(Jump Point Search),所以没忍住也给实现了一遍,耗费了国庆的一天假期 。说实话,在一般情况下这个算法的效率简直不是比A*star算法好了一丁点,基本上都快了几十到几百甚至上千倍,而且得到的也是最短路径。所以看到效果时我都吓了一跳,不过实现过程比较艰辛,国内关于此算法的介绍有限,去国外看的英文文章有点费劲,不过好在那篇文章(Jump Point Search Explained)提供了大量的步骤图,还有个demo可以随时调试。然后我就左试右试,把每种情况基本都摸清楚了,步骤也搞明白了,算是基本成型了吧?(原算法那篇论文有点看不明白,里面也没有提到具体节点的代价怎么计算,所以我还是沿用了A*算法的模式)还有一个问题没解决,就是被迫邻居节点可能同时一个方向出现两个,而我只处理了一个。
。说实话,在一般情况下这个算法的效率简直不是比A*star算法好了一丁点,基本上都快了几十到几百甚至上千倍,而且得到的也是最短路径。所以看到效果时我都吓了一跳,不过实现过程比较艰辛,国内关于此算法的介绍有限,去国外看的英文文章有点费劲,不过好在那篇文章(Jump Point Search Explained)提供了大量的步骤图,还有个demo可以随时调试。然后我就左试右试,把每种情况基本都摸清楚了,步骤也搞明白了,算是基本成型了吧?(原算法那篇论文有点看不明白,里面也没有提到具体节点的代价怎么计算,所以我还是沿用了A*算法的模式)还有一个问题没解决,就是被迫邻居节点可能同时一个方向出现两个,而我只处理了一个。
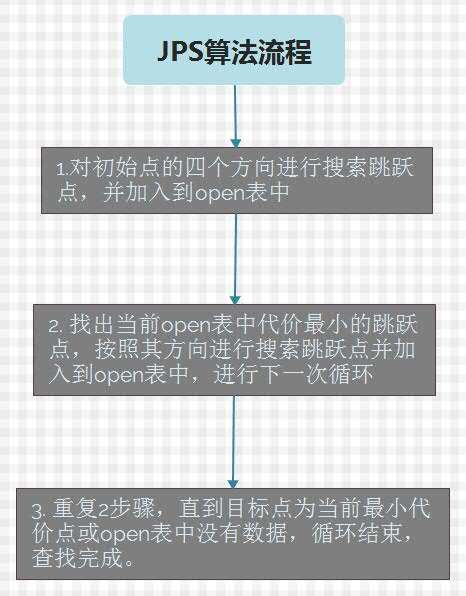
这个算法比较精妙,它直接跳过那些空白的(也就是直线方向没有障碍物的)点,大大减少了open表处理的数据,称之为跳跃点,跳跃点根据情况不同而有不同确定方法。其中最复杂的部分就是对于被迫邻居节点(forced neighbor)的处理了,由于没图不太好说,还是推荐去我之前提到过的那个网站(http://zerowidth.com/2013/05/05/jump-point-search-explained.html)看看比较好,一目了然。
我还试着做个流程图,感觉不太像。![]()
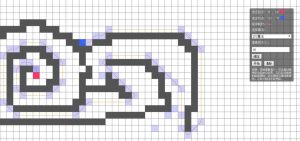
给个效果图:
后话:在实现过程中,还碰到了一个奇怪的“bug”,就是一部分数组的最后一个元素没办法得到,length也是少了1,但是打印出来的数组却是对的,找了好久原因也没找到,这个问题也影响了部分效率。结果去知乎上问,居然还被关闭了。